

더블리 링크드 리스트의 접근, 탐색, 삽입, 삭제 연산에 대하여 시간 복잡도를 알아보자
더블리 링크드 리스트의 접근, 탐색 연산
더블리 링크드 리스트의 접근, 탐색 연산은 싱글리 링크드 리스트의 접근, 탐색과 똑같다
head 노드부터 하나씩 다음 노드로 가면서
원하는 위치에 접근하거나
원하는 데이터를 가진 노드를 찾는다
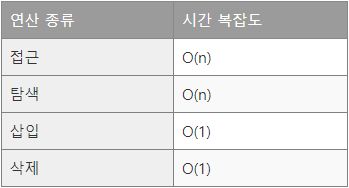
시간 복잡도는 리스트의 길이 n에 비례하므로 O(n)을 갖는다
더블리 링크드 리스트의 삽입, 삭제 연산
삽입 연산의 경우 특정 노드가 주어졌을 때, 특정 노드의 앞과 뒤 노드의 레퍼런스만 바꿔주면 된다
링크드 리스트의 길이와 상관없이 항상 일정한 시간이 걸리므로
시간 복잡도는 O(1)을 갖는다
삭제 연산도 마찬가지로 레퍼런스만 바꿔서 연결만 끊어주면 되므로
링크드 리스트의 길이와 상관없이 시간 복잡도는 O(1)을 갖는다
정리
조금 더 생각해보자
삽입, 삭제 연산은 O(1)의 시간 복잡도를 갖지만
삽입, 삭제를 하기 위해서는 삽입, 삭제할 특정 노드를 파라미터로 넘겨주어야 한다
따라서 삽입, 삭제할 노드를 먼저 탐색, 접근 연산을 통해서 가져와야 한다
탐색, 접근 연산은 O(n)의 시간 복잡도를 갖고
삽입, 삭제 연산 자체는 O(1)의 시간 복잡도를 가지므로
총 O(n+1)의 시간 복잡도를 갖는다
즉, 특정 노드에 삽입, 삭제를 하는 연산은 사실상 O(n)의 시간 복잡도를 갖게 된다
특수한 경우
특정 노드에 삽입, 삭제를 하는 연산은 O(n)의 시간 복잡도를 갖지만
그 특정 노드가 head나 tail이면 이야기는 달라진다
링크드 리스트는 head와 tail의 정보를 저장하고 있기 때문에
head, tail 노드에 한 번에 접근할 수 있다
따라서 head, tail에 삽입, 삭제를 하는 경우
head, tail 노드에 한 번에 접근하여 삽입, 삭제를 하는 시간을 고려하면
시간 복잡도는 O(1+1) => O(1)이 된다
최종 정리

싱글리 VS 더블리 링크드 리스트

싱글리 링크드 리스트와 더블리 링크드 리스트 연산의 시간 복잡도는 대부분 동일하다
하지만 tail 노드의 삭제 연산의 경우는 다르다
싱글리 링크드 리스트의 삭제 연산은 지우려는 노드의 바로 전 위치의 노드를 파라미터로 받아야 한다
그렇기 때문에 tail 노드를 삭제하기 위해서는 tail 전 노드에 접근해야 한다
tail 전 노드에 접근해야 하기 때문에 O(n)을 갖는다
더블리 링크드 리스트의 삭제 연산은 지우려는 노드 자체를 파라미터로 받는다
링크드 리스트는 tail노드의 정보를 가지고 있기 때문에
tail 노드를 바로 파라미터로 넘겨주면 tail 노드를 삭제할 수 있다
링크드 리스트를 사용해야 하는 경우
tail 노드를 많이 삭제해야 한다면
싱글리 링크드 리스트보다 더블리 링크드 리스트를 사용하는 게 더 효율적이다
'프로그래밍 > 자료구조&알고리즘' 카테고리의 다른 글
| 이진 트리의 종류 (0) | 2021.10.12 |
|---|---|
| Direct Access Table과 Hash Table (0) | 2021.10.05 |
| 싱글리 링크드 리스트 연산의 시간 복잡도 (0) | 2021.09.28 |
| 시간복잡도 분할 상환 분석(동적 배열의 추가 연산) (0) | 2021.09.25 |
| 리스트는 사실 배열?(3/3) (0) | 2021.09.11 |
