이진 트리란?
각 노드가 최대 2개의 자식 노드를 가질 수 있는 트리이다
정 이진 트리 (Full Binary Tree)
모든 노드가 2개 또는 0개의 자식을 갖는 이진 트리이다

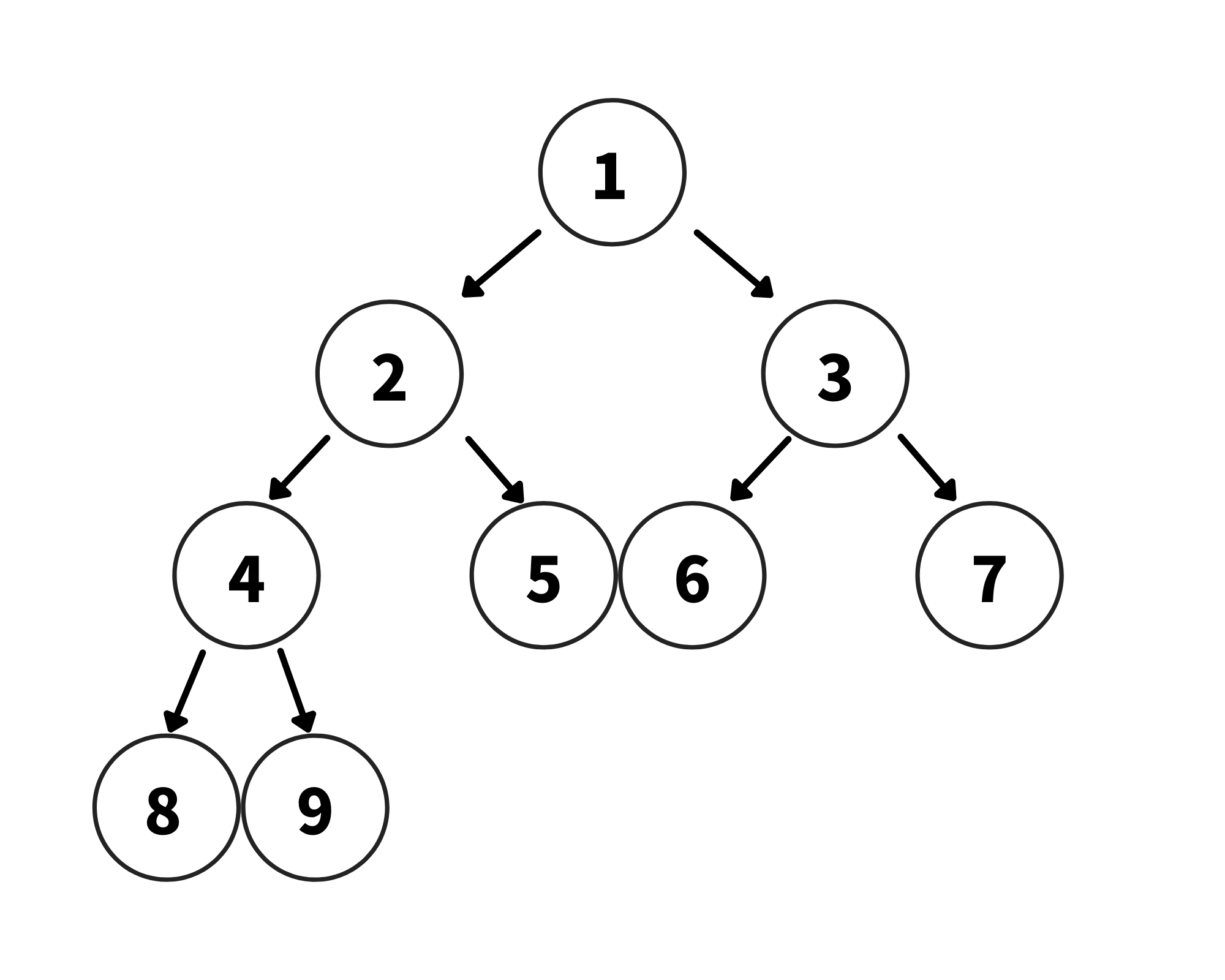
아래 그림처럼 3의 자식이 하나밖에 없는 경우는 정 이진 트리가 아니다

완전 이진 트리 (Complete Binary Tree)
마지막 레벨 직전의 레벨까지는 모든 노드들이 다 채워진 트리이다
마지막 레벨에서는 노드들이 모두 채워질 필요가 없더라도
왼쪽부터 오른쪽으로 노드들이 채워져야 한다
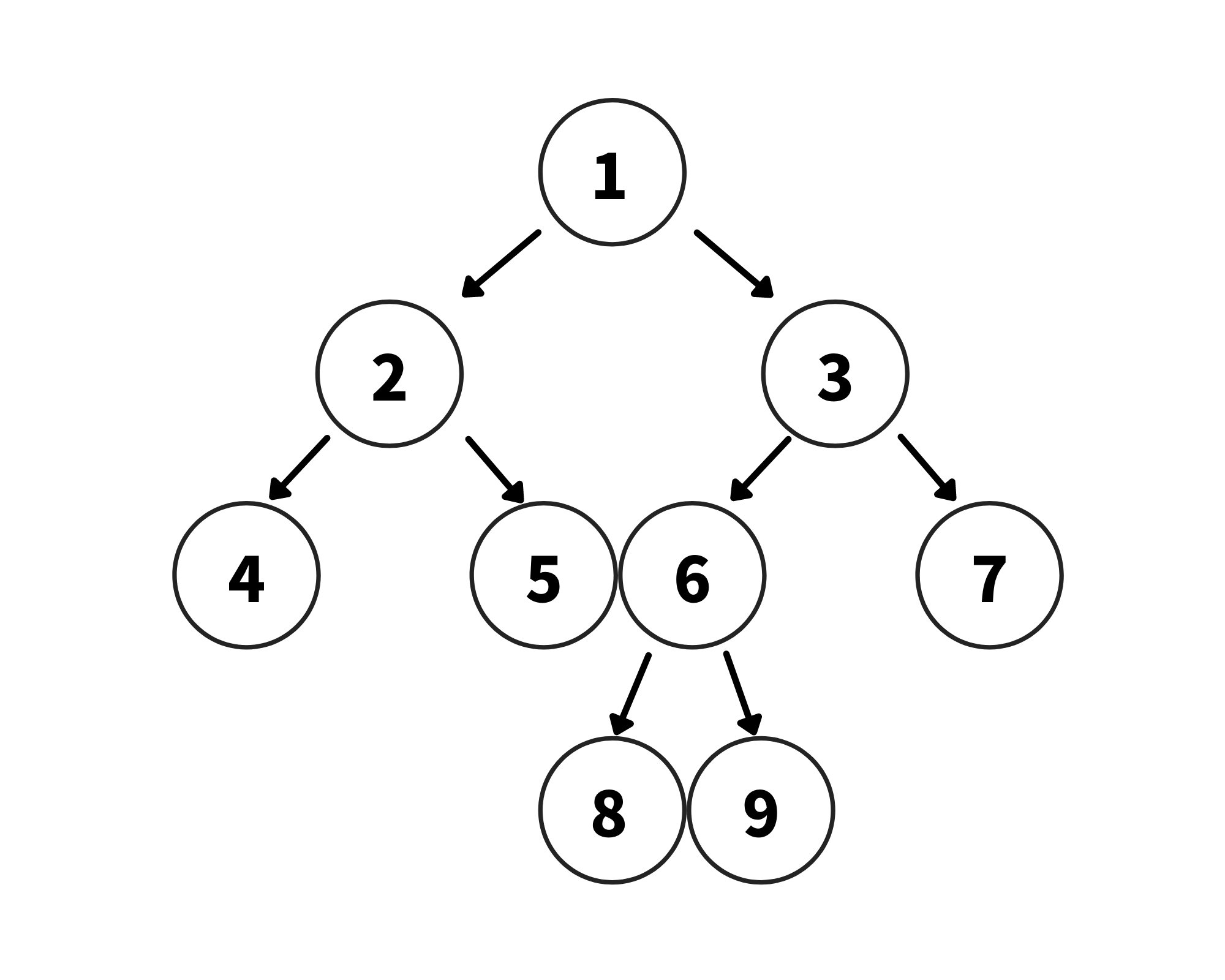
아래 그림처럼 마지막 레벨 직전까지의 레벨이 모두 채워졌지만
마지막 레벨에서 노드가 왼쪽에서부터 채워지지 않은 경우는 완전 이진 트리가 아니다
완전 이진 트리의 높이
완전 이진 트리에는 높이와 관련된 성질이 있다
완전 이진 트리 안에 n개의 노드가 저장되어 있다면
완전 이진 트리의 높이는 항상 lg(n)에 비례하게 된다
완전 이진 트리의 높이를 h라고 하자
완전 이진 트리는 마지막 레벨 직전 레벨까지는 모두 노드로 가득 채워져 있고
레벨이 하나 증가할 때마다 담을 수 있는 노드의 개수가 이전 레벨의 노드의 2배가 된다
이 성질을 이용하여 n과 h의 관계를 나타낼 수 있다
$$2^h <= n <= 2^{h+1} - 1$$
$$= 2^h <= n < 2^{h+1}$$
$$= h <= lg(n) < h+1$$
노드 수가 n개인 완전 이진 트리의 높이는 $$h <= lg(n)$$를 만족하는 정수 중 최대의 정수이다
또한, 현재 노드 수보다 노드 수가 2배 이상이 되었을 때 높이도 하나 더 올라가게 된다
즉, 완전 이진 트리의 높이는 O(lg(n))인 것이다
포화 이진 트리 (Perfect Binary Tree)
포화 이진 트리는 모든 레벨이 빠짐없이 전부 노드로 채워져 있는 이진 트리 이다
포화 이진 트리는 정 이진 트리와 완전 이진 트리의 특성을 모두 갖고 있다

트리의 높이 h, 와 노드 수 n의 관계를 표현하면
$$n+1 <= 2^{h+1}$$이렇게 나타낼 수 있다
'프로그래밍 > 자료구조&알고리즘' 카테고리의 다른 글
| 스택 - 후위표기식 (0) | 2022.02.07 |
|---|---|
| 스택 - 괄호검사, DFS (0) | 2022.02.06 |
| Direct Access Table과 Hash Table (0) | 2021.10.05 |
| 더블리 링크드 리스트 연산의 시간 복잡도 (0) | 2021.10.02 |
| 싱글리 링크드 리스트 연산의 시간 복잡도 (0) | 2021.09.28 |
